Dijkstra算法,中文翻译为迪杰斯特拉算法,是在带权有向图G = (V, W) (V是节点的集合,W是边上权值的集合,在集合W中,不直接相连的节点间的距离标记为无穷大)中求某个节点到其余节点之间最短路径的经典算法。该算法的核心思想是将图中所有的节点划分为2个集合,集合S包含已经找到最短路径的节点,集合U包含尚未找到最短路径的节点的距离(初始值全部设定为无穷大)。从某一点v开始采用广度优先遍历思想对图进行遍历,每找到一个节点的最短路径,就将该节点从集合U中移除,并加入到集合S中,直到最后U变为空集,S包含图中所有的节点到出发点的最小距离。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长… Read more
May 2015
Dijkstra算法C#演示程序
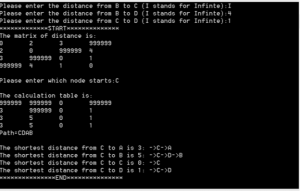
最近学习Dijkstra算法和C#,用C#写了一个Dijkstra算法的演示程序。图中的节点要求使用26个字母来表示。节点之间的距离为整数,不相邻节点输入”I”或”i”来代表Infinite。该程序移除了输入的冗余,并且显示输入节点和距离后的邻接矩阵。同时会在最终结果给出前,打印出 Dijkstra算法的计算过程表和最短路径点的次序(path数组)。在代码中给出了详细的注释,对于学习Dijkstra算法的人具有一定帮助。
运行效果图:
 … Read more
… Read more