Dijkstra算法详解

Dijkstra算法，中文翻译为迪杰斯特拉算法，是在带权有向图G = (V, W) （V是节点的集合，W是边上权值的集合，在集合W中，不直接相连的节点间的距离标记为无穷大）中求某个节点到其余节点之间最短路径的经典算法。该算法的核心思想是将图中所有的节点划分为2个集合，集合S包含已经找到最短路径的节点，集合U包含尚未找到最短路径的节点的距离（初始值全部设定为无穷大）。从某一点v开始采用广度优先遍历思想对图进行遍历，每找到一个节点的最短路径，就将该节点从集合U中移除，并加入到集合S中，直到最后U变为空集，S包含图中所有的节点到出发点的最小距离。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。

Dijkstra算法的过程：

1. 选取某个节点v作为出发点，从出发点到出发点距离为0，即找到最小路径。将该出发点从集合U中移除并加入到集合S中。
2. 在集合W中查看出发点v到集合U中各个节点的距离。找出距离最小的节点k（到k的最短路径找到），将k从集合U中移除并加入到集合S中。
3. 以k作为中间点，在W中查看从k到U中节点m的距离，如果m在W中的值小于m在U中的值（k和m直接连接），将m在W中的值与k在U中的值相加（从v出发经过k到达m的距离），再将相加结果与W中v到m的值(v不经过中间点到m的距离)对比大小，选取较小的值跟新k在U中的数据。
4. 在U中找出数值最小的节点n，该值即为v到n的最短路径。将n从集合U中移除并加入到集合S中。把n作为中间点重复第3、4步，直到U中所有的节点都移动到S中。

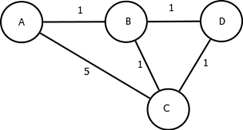
图1

Dijkstra算法的手算方法

如图1，从节点A开始。首先我们创建一个表，用该表记录每次运算的值。该表表头代表了集合U中包含的节点（未找出最短路径节点：A、B、C、D）。第２行将各节点的距离，初始化为无穷大，用INF表示。

点A是出发点，自身到自身的路径最短，为0，即A到Ａ的最短路径找到。在Ａ列的第２行输入０，并用下划线标出，表明将Ａ从Ｕ中移除。在表的第２行最左侧写A，表示将A加入集合S。

建立表格第3行。此时集合U中包含{B、C、D}，由图可知A->B的距离为1（查询集合W），更新B列的数值，写入第3行。由图可知A->C的距离为5，更新B列的数值，写入第3行。由图可知A->D不可直达，标记为INF。在表第3行中对集合U中所拥有的元素{1，5，INF}求最小值，得到B，此时B列第3行数据即为A->B的最小路径。对B列第3行数据加下划线标识出，即将B移出集合U。同时在第3行最左端写B，即将B加入集合S中。

建立表格第4行。此时集合U中包含{C、D}，节点B为中间点。由图可知B->C的距离为1，而A->B的距离保存在表B列中，是1，则A->B->C的距离为1+1=2。由表C列第3行数据可知目前到达C的距离为5（A直接到达C）。求两条路径的最小值min(5,1+1)=2;更新C列数据，将2写入C列第4行。由图可知B->D点的距离为1，则A->B->D的距离为1+1=2，而A->D不可直接抵达，故而取值无穷大INF（该值记录在集合W中，此时该值等于表中D列数据）。求两条路径的最小值min(INF，1+1)=2。更行D列数据，将2写入到D列第4行。对集合U中的数据取最小值，C和D均为2，任选一个，该节点到A的最短距离即被计算出来。比如选C。对C进行标记。

重复上面的操作，建立表格第5行。此时集合U中只包含{D}，节点C为中间点。由图可知C->D的距离为1。而A->C的最短距离已经求出，在上表中C列第4行，为2（经过节点B）。故A->B->C->D的距离为2+1=3。表中D列第4行记录到达D点的最小路径为2（通过B点），求两条路径的最小值min(2,2+1)=2。即D点的最小路径为2，将2写入D列第5行并对D列第5行进行标记。此时集合U为空集，集合S中的元素为{A、B、C、D}，计算完毕。表中第5行所记录数据即为A点到各点的最小路径值。

具体路径（经过的节点）可以通过回溯法求出。在最后一张表中找到要求点所在的列，从下向上回溯，当数值发生变化时，跳转到所在行所对应的S集合中的元素所在的列，记录下该点，然后继续回溯，直到到达出发点。

如求到达C点的具体路径，从C列第5行向上回溯，到达第3行时数值发生变化，第3行对应为S集合中的B，则从B列第3行向上回溯，到达B列第2行，数值发生变化，第2行所对应的集合S中的元素为A，是起点，回溯完成。具体路径即为A->B->C。

本思路所对应的C#源代码请参看《Dijkstra算法C#演示程序》一文。